Das tun wir insbesondere mit "SQL" und dem gratis Programm "SQLiteman"
SQL
SQL ist eine Datenbanksprache, die zur Definition von Datenstrukturen und zur Bearbeitung und Abfragung von darauf basierenden Datenbeständen verwendet wird.
Die Syntax der Sprache ist relativ einfach aufgebaut und an die englische Umgangssprache angelehnt.
Fast alle gängigen Datenbanksysteme unterstützen SQL, allerdings in unterschiedlichem Umfang.
Die Bezeichnung SQL ist eine Abkürzung für "Structured Query Language" und bedeutet auf Deutsch "strukturierte Abfragesprache".
Sprachelemente/Statements
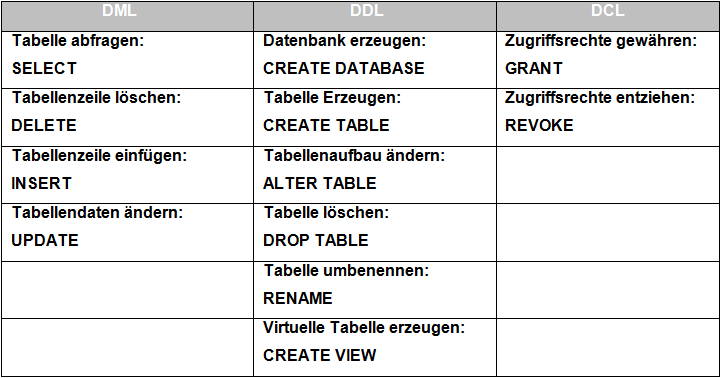
Die einzelnen Elemente lassen sich in drei Kategorien unterteilen.
-DML: Data Manipulation Language (Datenverarbeitungssprache)
Befehle zum Abfragen, Einfügen, Ändern, und Löschen der Daten.
-DDL: Data Definition Language (Datenbeschreibungssprache)
Befehle zum Anlegen, Ändern, und Löschen von Datenstrukturen (Datenbankschema).
-DCL: Data Control Language (Datenaufsichtssprache)
Befehle für die Zugriffskontrolle.
Mit verschiedenen Abfragen werden die gespeicherten Daten abgerufen, das heißt, die Daten werden dem Benutzer oder einer Anwendersoftware zur Verfügung gestellt.
Das Ergebnis einer Abfrage wird als Tabelle dargestellt und kann auch wie in einer Tabelle bearbeitet und weiterverwendet werden.
Hier einige Beispiele zu Abfragen, unterteilt in den drei Kategorien:
Eine mögliche Abfrage wäre nun:
SELECT *
FROM "Tabellen Name";
Diese Abfrage (oder Statement) listet alle Spalten und Zeilen der angegebenen Tabelle auf.
Um der Tabelle eine Zeile hinzuzufügen, wird folgendes Statement verwendet:
INSERT INTO "Tabellen Name" ("Spalte1","Spalte2", ....)
VALUES ("Wert1", "Wert2", ...);
Um nun eine Zeile aus einer Tabelle zu löschen, wird folgendes Statement benutzt:
DELETE FROM "Tabellen Name"
WHERE "Bedingung";
Datentypen
SQL liefert eine ganze Reihe standardisierter Datentypen. Diese werden zum Beispiel mit den Statements "CREATE TABLE" und "ALTER TABLE" verwendet, um anzugeben, welchen Datentyp die jeweiligen Spalten haben.
integer:
Ganze Zahl, die positiv oder negativ sein kann. Die jeweilige Grenze, wie groß eine Zahl sein darf, ist vom Datenbanksystem definiert.
numeric:
Festkommazahl (positiv oder negativ), die eine bestimmte Länge an Stellen haben kann, darin sind auch die Nachkommastellen inbegriffen.
float:
Gleitkommazahl (positiv oder negativ), die eine maximale Länge an Nachkommastellen hat.
real:
Gleitkommazahl (positiv oder negativ), deren Genauigkeit vom jeweiligen Datenbanksystem definiert ist.
character oder char:
Zeichenkette (Text) mit einer bestimmten Anzahl an Zeichen.
varchar oder character varying:
Zeichenkette (Text) mit variabler Länge
date:
Datum (ohne Zeitangabe)
time:
Zeitangabe (evtl. inklusive Zeitzone)
timestamp:
Zeitstempel (umfasst Datum und Uhrzeit), meistens mit Milisekundenauflösung
boolean:
Variable, die die Werte true oder false annehmen kann.
blob (binary large object):
Binärdaten, die eine maximale Länge von Bytes haben.
clob (character large object):
Zeichenkette, die eine maximale Länge von Bytes hat.
Falls kein Wert bekannt ist oder kein Wert gespeichert werden soll, können Attribute auch den Wert NULL haben.
Redundanz
In einer Datenbank sollen keine Redundanzen auftreten.
Das bedeutet, dass jede Information, also z.B. eine Adresse, nur genau einmal gespeichert wird.
In einigen Fällen ist die Performance der Datenbank besser, wenn sie nicht vollständig normalisiert wird, das heisst, Redundanzen werden bewusst in Kauf genommen, um zeitaufwendigere Verknüpfungen der einzelnen Tabellen zu verkürzen und so die Geschwindigkeit der Abfrage zu erhöhen.
Schlüssel/Key
Während Informationen auf viele Tabellen verteilt werden müssen, um Redundanzen zu vermeiden, sind die Schlüssel ein wichtiges Mittel, um die einzelnen Informationen miteinander zu verknüpfen.
Jeder Datensatz hat also eine eindeutige Nummer, um ihn zu identifizieren. Diese Identifikationen werden als Schlüssel bezeichnet.
Wenn ein Datensatz in anderen Zusammenhängen benötigt wird, wird einfach nur der jeweilige Schlüssel angegeben, daraus ergeben sich dann alle restlichen Informationen.
So kann es sich nun ergeben, dass manche Datensätze nur aus Schlüsseln bestehen, die erst mit den Verknüpfungen verständlich werden. Der eigene Schlüssel wird dabei als Primärschlüssel bezeichnet, die anderen Schlüssel, die auf Primärschlüssel anderer Tabellen verweisen, werden als Fremdschlüssel bezeichnet.
Referentielle Integrität
Definition:
Die referentielle Integrität besagt, dass Attributwerte eines Fremdschlüssels auch als Attributwert des Primärschlüssels vorhanden sein müssen.
Das bedeutet: Fremdschlüssel müssen IMMER auf existierende Datensätze verweisen.
Diese wichtige Funktion sollte bereits von der Datenbank überwacht werden.
Löschweitergabe:
Die referentielle Integrität besagt, dass Attributwerte eines Fremdschlüssels auch als Attributwert des Primärschlüssels vorhanden sein müssen.
Das bedeutet: Fremdschlüssel müssen IMMER auf existierende Datensätze verweisen.
Diese wichtige Funktion sollte bereits von der Datenbank überwacht werden.
Löschweitergabe:
Wird ein Datensatz gelöscht, werden die abhängigen Daten auch in der verknüpften Tabelle gelöscht.
Änderungsweitergabe:
Wird ein Datensatz geändert, wird diese Änderung auch in der verknüpften Tabelle ausgeführt
Änderungsweitergabe:
Wird ein Datensatz geändert, wird diese Änderung auch in der verknüpften Tabelle ausgeführt
Beziehungen zwischen Tabellen
Es gibt im Wesentlichen drei Arten von Beziehungen:- 1:1 Für jeden Datensatz in der Primärtabelle gibt es nur einen einzigen Datensatz in der Fremdtabelle
- 1:N Für jeden Datensatz in der Primärtabelle gibt es einen oder mehrere verwandte Datensätze in der Fremdtabelle
- N:n Für jeden Eintrag in der Primärtabelle gibt es viele verknüpfte Datensätze in der Fremdtabelle und umgekehrt